When feeling positive is being “in the zone”: How challenge optimality causes changes in positive affect and flow

Introduction

Video game researchers have long sought to understand how difficulty impacts player experience. For decades, psychologists have investigated the flow state (hereafter just ‘flow’; Csikszentmihalyi, 1975). According to the flow theory, a cognitive or motor task is likely to induce flow if it matches the person’s skill level (optimal challenge). During flow, a person experiences intense attentional focus and a distorted sense of time. They also tend to become intrinsically motivated to go through the experience again (Csikszentmihalyi & Csikszentmihalyi, 1992). Thus, many researchers have sought to induce flow in players. One method is dynamic difficulty adjustment (DDA) - they programmed games to adjust their own difficulty, i.e., increase difficulty if the player performs well and decrease difficulty if the player performs poorly, presumably resulting in more optimal challenges. Empirical studies showed that DDA can improve player flow and other player experience metrics (for a review, see Zohaib, 2018).

Following this, many prominent video game franchises have adopted DDA. The Mario Kart series, for example, involve races in which players can utilise randomly drawn items to gain advantages. Players who are falling behind have higher probabilities of drawing powerful items—making the game easier when a player is performing poorly (Nintendo, 2011). Other games offer assistance if the player is struggling. The 2020 game Crash Bandicoot 4: It’s about Time (Activision, 2020) offered the player free power-ups once the player has failed a level for more than a set number of times. There is a need to investigate how DDA impacts player experience. It is known that DDA can impact experiential variables other than flow, such as player confidence (Constant & Levieux, 2019), user satisfaction (Lora et al., 2016) and sense of autonomy should the player be aware of DDA’s presence (Baldwin et al., 2014). Moreover, game difficulty is known to influence emotional states (Liu et al., 2009). Based on this literature, we seek to further our understanding of the effects of DDA, by focusing on the interplay between flow state and positive affect (hereby PA). How does DDA affect PA? How are flow and PA (both psychological states DDA can influence) related? Furthermore, how might flow and PA impact each other in dynamic ways?

To answer these questions, we review the literature and draw upon (a) the flow theory and (b) the theoretical literature on PA. Based on the finding that flow requires moderate levels of perceived threats (e.g., Peifer et al., 2011) and that PA is linked to the absence of threats (Fredrickson, 2001), we formulated hypotheses by arguing that flow and PA are negatively linked to each other under DDA-elicited optimal difficulty. After that, we conducted two experiments using Tetris, one of the most used games in experimental game research. This choice of experimental task ensures that our results can be easily compared with past studies’. The results provided support for our hypotheses. This result contributes to an emerging literature on more dynamic models of flow, i.e., how various psychological variables change over time during flow (Kotler et al., 2022; Weber et al., 2009). We also briefly discuss the implications of our findings for video game design.

DDA and Flow Research: The Background

Flow experience has been hailed as a key goal of game design (Chen, 2007; Hunicke, 2005). The concept was introduced by Csikszentmihalyi, in his seminal 1975 book “Beyond Boredom and Anxiety”. Csikszentmihalyi described the flow state (hereby as “flow”) as “an optimal state of consciousness where humans feel their best and perform at their best”. Flow is said to be immensely pleasurable and during flow, people demonstrate optimal performance. His research showed that flow can be found across various fields, such as sports, dance, and chess. Subsequent research also showed that flow can be found across cultures and social classes (Csikszentmihalyi & LeFevre, 1989; Nakamura & Csikszentmihalyi, 2014).

Research has identified six characteristics of flow experience (FE): high level of attentional focus, total absorption, reduction of self-reflective cognition and awareness of one’s own body, a distorted sense of time, a heightened level of task performance, and positive emotional states, particularly high levels of intrinsic motivation. Three other characteristics have been identified, but more commonly regarded as ‘preconditions’ of flow as a mental state. These include clear goals, clear feedback, and optimal challenge (Csikszentmihalyi, 1990; Csikszentmihalyi & LeFevre, 1989). Several reviews have been published on theoretical models of flow (Fisher et al., 2021; Khoshnoud et al., 2020; Kryston et al., 2018; Peifer et al., 2022; Van Der Linden et al., 2021).

Many researchers have adopted a neuroscientific approach and defined flow as specific neural states involving the attentional and often reward networks (Dietrich, 2004; Weber et al., 2009). Dietrich (2004), for instance, discussed the concept of hypofrontality, arguing that flow is characterised by suppressed explicit processing. While there is still debate regarding the precise neuroscientific nature of the mental state of flow, researchers converge on the idea that flow is a special neural state involving the attentional and reward networks, characterised by high attentional focus and a distorted sense of time. This shall be the core conceptualisation we adopt.

Many researchers consider flow to be ‘the ideal player experience’. From a theoretical standpoint, flow is associated with pleasure. Empirical studies have also shown that it is linked to intense intrinsic motivation (Nacke & Lindley, 2010; Nakamura & Csikszentmihalyi, 2014). Game designers seek to make the gaming experience pleasurable and motivate players to continue playing (Hunicke, 2005; Khalis et al., 2022). In fact, Sherry (2004) suggested that “some might comment that Csikszentmihalyi seemed to have video games in mind when he developed the concept of flow’’ (p. 339), noting that “(video) games possess ideal characteristics to create and maintain flow states in that the flow experience of video games is brought on when the skills of the player match the difficulty of the game’’ (p. 340). This view is corroborated by empirical evidence. Studies have both conducted player observation (Bowman & Boyan, 2008; Bowman & Sherry, 2006) and utilised online surveys (e.g., Su et al., 2016). Player flow is positively linked to various indicators of motivation to play (De Jans et al., 2019; Ho & Kuo, 2010; Hunicke, 2005; Staiano et al., 2019), including self-reported motivation (De Jans et al., 2019; Ho & Kuo, 2010), player loyalty (Su et al., 2016) and hours spent playing (Lee & LaRose, 2007). Moreover, studies showed that flow in gaming (or at least some of its components) is positively associated with video game addiction, which involves excessively high motivation to play (Chou & Ting, 2003; Hull et al., 2013; Liu & Chang, 2016).

The literature highlights how Dynamic Difficulty Adjustment (DDA) is an important feature of games (Afergan et al., 2014; Liu et al., 2009; Park et al., 2014). There are multiple approaches to DDA (for a review, see Zohaib, 2018). Nonetheless, they are all based on optimal challenge being a key trigger of flow (Andrade et al., 2005; Zohaib, 2018).

Using DDA, the game tracks the player’s performance, using it as a proxy of ‘how difficult the game is to the player’—low performance indicates overly high difficulty and high performance indicates overly low difficulty. The game also adjusts difficulty parameters based on performance indicator(s)—it will reduce difficulty if performance is low and increase difficulty if performance is high. Difficulty can be measured using many factors, e.g., the amounts of health “enemies” have in a shooter game, with higher amounts of health suggesting high difficulty.

DDA should result in higher likelihood of optimal challenge. The DDA literature has more in-depth discussions on the various aspects of DDA. Generally, DDA has been shown to increase player flow (Huskey et al., 2022; Keller & Bless, 2008; Tozman et al., 2015; ). Thus, some prominent video game franchises have adopted DDA in their designs. In theoretical works, DDA has also seen wide use for experimentally inducing flow (Csikszentmihalyi & LeFevre, 1989; Nakamura & Csikszentmihalyi, 2014).

Hypothesis Development

We consider how DDA causes changes in positive affect (PA), another heavily discussed variable with regards to player experience (Bowey et al., 2015; Gajadhar et al., 2008; Nacke & Lindley, 2010). In the most basic sense, PA can be defined as any emotional experience that reflects a form of pleasurable engagement with the surroundings (Clark et al., 1989; Coffey & Warren, 2020; Pressman et al., 2019), subjectively experienced as they emerge from basic processes, which include specific changes in facial expressions (Nacke & Lindley, 2010), vocal expression (Revord et al., 2021), and other physiological changes. Such diverse psychophysiological states as happiness, excitement, and gratitude are all grouped under “PA”.

The link between flow and PA is well-established, and some researchers consider PA to be a part of the flow state. Even in the earliest flow research, it was reported that participants typically described the (flow) experience as highly pleasant (Csikszentmihalyi, 1975, 1990; Csikszentmihalyi & LeFevre, 1989). Conceptualisation of flow typically involves the reward networks, which is associated with PA. However, the two are not identical, as positive emotional experience also encompasses a series of cognitive and physiological changes outside the reward network (e.g., Shiota et al., 2014). Many studies have been conducted and reported positive correlations between flow and PA measures. The correlations are indicative of moderate to strong relations, without the two being the same construct (Chiang et al., 2011; Cseh et al., 2015; De Manzano et al., 2010; Huang et al., 2017; Konradt et al., 2003; Rogatko, 2009; Shoshani & Yaari, 2021). A few studies even reported weaker correlation, such as Rodríguez‐Ardura & Meseguer‐Artola (2017).

Studies that use non-self-report methods also report positive links between flow and PA. Nacke and Lindley (2010), for instance, conducted an experimental study and reported that video game levels designed to elicit flow (i.e., gradually increasing difficulty over time as the player learned) instead of boredom (i.e., difficulty remaining the same over time) elicited higher levels of PA. More recently, Huskey et al., (2018) used experimental manipulations and fMRI to show that high levels of skill-challenge compatibility elicited higher levels of functional connectivity in the reward networks. In summary, evidence converges to suggest that flow and PA are positively linked. So far, relatively few studies have investigated causal links between flow and PA. Self-report studies did not utilise experimental manipulations and thus cannot provide support for causality. Therefore, our first objective is to corroborate the findings of Huskey and colleagues (2018) and several others who showed that challenge optimality activates (causes) reward-related brain structures (Ulrich et al., 2014, 2016):

H1: Optimal challenge causes greater levels of positive emotional experience, as compared to overly low or overly high difficulty.

H2: Current positive emotional experience is positively associated with current flow, regardless of difficulty.

We also consider how PA changes at the within-person level. Specifically, we draw on the Broaden-and-Build (B&B) Theory. The B&B Theory is a widely discussed theoretical model in research related to positive emotions. The basic idea is that positive affective experience is a psychological state that evolved as a response to safe environments. When threats are present, humans experience negative emotions such as fear and anxiety to prompt the body to engage in defensive behaviours such as fleeing or fighting (Jansen et al., 1995; Levenson et al., 1991). In the presence of rewards and absence of threats, people experience positive emotional experience which encourages playful, exploratory behaviour, prompting the person to engage in social interactions or activities that build social and/or cognitive resources (Carver, 2003; Fredrickson, 2001, 2004, 2013; Isen, 1987). Research shows that positive emotional experience elicits (for example) broadening attention (Wadlinger & Isaacowitz, 2006). Such gains in personal resources, in turn, are likely to lead to increased likelihood of experiencing more positive emotional experience in the future (Burns et al., 2008; Ramsey & Gentzler, 2015). This results in an “upward spiral” effect, where positive emotional experience leads to greater likelihood of positive emotional experience in the future. Longitudinal research confirmed this (Fredrickson, 2000). However, the B&B theory is not primarily a cyberpsychology theory. Thus, evidence for the “upward spiral” of PA is relatively scant in the cyberpsychology literature. We would thus like to replicate this finding in a gaming context:

H3: Current positive emotional experience is positively associated with future positive emotional experience, regardless of difficulty.

Crucially, we investigate the link between current PA and future levels of flow. Given the established positive link between PA and flow, it might be tempting to suggest that the link is universally positive. However, we would like to argue for a more nuanced view. We use the concept of difficulty as the starting point. Difficulty can be conceptualised in many ways. Constant and Levieux (2019), for instance, conceptualised “optimal difficulty” as a state where the player has close to 50% chance of succeeding (thus an around 50% chance of failing). Some researchers have conceptualised difficulty in the same way (Aponte et al., 2009; Constant et al., 2017). Aponte et al. (2011) defined “difficulty” formally, as the probability of succeeding at a task, with lower probability indicating higher difficulty:

D(a, c) = Probability{Lose(c)|Level(a, c)}

Other studies utilised similar concepts of difficulty (Fraser et al., 2014; Isaksen et al., 2015) and generally agreed that an optimally difficult task offers both chances for success and chances for failure. Such definitions, based on observed probability (Herbrich et al., 2006; Mourato & Santos, 2010), makes it easy to empirically quantify difficulty, but ignores the fact that difficulty has a subjective component (Tamor, 1981). Gallego-Durán and colleagues (2018) proposed a more nuanced definition, in which difficulty reflects the amount of effort (or progress) required to succeed. An extremely easy task requires little to no effort, while an impossibly difficult one would end in failure even if the person invests maximum effort. The objective probability of success, while not the same as difficulty, should be strongly tied to it, likely usable as a proxy measure. This definition agrees with past flow studies where difficulty was typically operationalised as the likelihood to succeed at the given task. It also echoes the finding that flow is associated with moderate difficulty and moderate levels of stress (Peifer et al., 2011, 2014)—a person experiencing flow needs to exert effort.

The presence of potential failure indicates threats. Crucially, high levels of positive emotional experience signal the absence of threats. According to the B&B theory, entering a positive emotional state is evolutionarily adaptive only when threats are absent in the environment. For example, when there is a predator capable of threatening human lives, entering a state that encourages approach and exploration is maladaptive. Instead, humans need to enter negative emotional states such as fear, to prompt fight-or-flight and other defensive behavioural responses. The B&B literature has shown that entering positive emotional experience subsequently elicits behaviours indicative of the perception of non-threatening environments (Conway et al., 2013).

This means current PA might reduce an activity’s perceived difficulty at later time points, by virtue of being associated with the absence of threats, undermining the perception of potential failures, which are important for flow. How this impacts flow should be dependent on difficulty conditions: For players under overly low or optimal difficulty, a reduction in perceived difficulty would draw them away from the optimal perceived difficulty, resulting in the reduction of flow. For the players under overly high difficulty, however, a reduction in perceived difficulty would draw them closer to the optimal perceived difficulty, resulting in an increase in flow. Conceptually, what we hypothesise is akin to a negative feedback loop: We think of PA as a correlate of flow, both induced by challenge optimality. However, some aspects of PA might be unfavourable for continual flow, causing current PA to be negatively associated with the levels of flow at later time points. Part of this feedback loop is moderated by challenge optimality, in that the negative effect of PA on later flow is particularly prominent in conditions of low or optimal difficulty.

While the literature has little to say about this possibility, there is some evidence in accordance with our idea. Constant and Levieux (2019) showed that DDA (compared to no DDA) increased players’ subsequent confidence in their own abilities to win. This could even be tied to the more general literature on self-efficacy. Past experience of success has been shown to improve a person’s self-efficacy, which by definition involves a person’s perception that they are likely to succeed (Tierney & Farmer, 2011; D. S. Wu et al., 2014). Other studies in related literature have documented that self-efficacy could sway a person’s perception of how difficult a task is (Schwarzer & Renner, 2000). Our idea that PA might reduce flow in some situations may also explain why some studies report weak correlations between PA (or other constructs that reflect positive emotions) and flow (e.g., Rodríguez‐Ardura & Meseguer‐Artola, 2017). Thus,

H4a: When difficulty is too low or optimal, past positive emotional experience is negatively associated with current flow.

H4b: When difficulty is too high, past positive emotional experience is positively associated with current flow.

In statistical terms, this means we are hypothesizing a moderation effect, with difficulty setting being the moderator, exerting a moderation effect on the link between current PA and future flow. Our hypotheses are summarized in Figure 1.

Figure 1. The Basic Model for the Current Study.

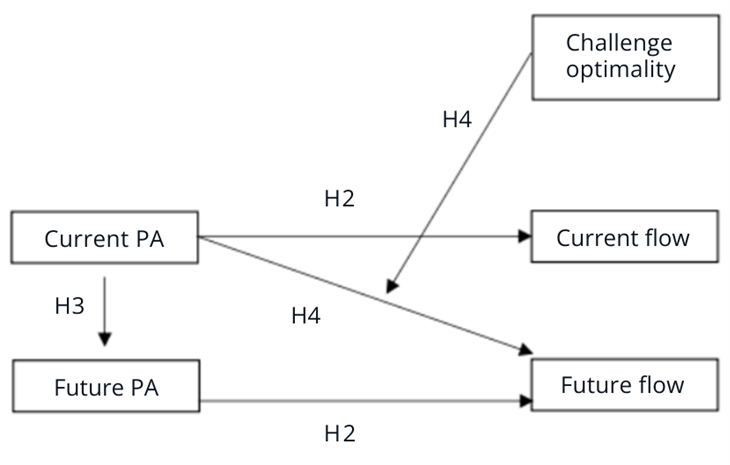Note. The hypothesis on causal relation between challenge optimality (H1)
would be evaluated by comparing PA across the three experimental groups.

Study 1

Methods

Participants

A total of 144 participants (approximately 54% male; 46% female) were recruited over the course of 2 semesters in the second half of 2019, through advertising to the cohort of undergraduate students who attended an entry-level management course. The University of New South Wales ethics committee approved of the methods employed in the research protocol and all the participants signed a form to indicate their consent to participate before the experiment commenced. Each student was rewarded with credits for their course upon study completion.

Experimental Task

The experimental task consisted of a modified version of the game Tetris (Burgiel, 1997) played via MATLAB. In Tetris, the player’s goal is to arrange “falling” objects so that they end up constituting fully filled lines at the bottom of the playing field. An object’s vertical position gets closer to the bottom at a steady rate and stops only if it reaches the bottom or is blocked by an already stopped object. When the object stops, a new object is spawned at the top of the playing field and the player’s control switches to the new object. The player can control the moving object’s horizontal positions or rotate it in 90° steps using assigned keys on the keyboard. Scores are obtained when a player manages to complete one or more row(s) when an object stops. Filled rows will be removed from the playing field. In the normal mode, the difficulty level (measured by the speed at which the active object falls) increases each time a set number of rows have been cleared. The game ends when new objects cannot be spawned, usually because the player has failed to clear rows, causing uncleared objects to accumulate and obstruct the spawn point. When the game ends, all blocks turn grey and the score is reset to zero (punishment), though players could see their high scores (the highest score they have ever attained) at the top right corner. The player has a clear goal (to reach the highest score possible) and clear feedback (their high scores are displayed to them). Tetris was chosen because it has proven to be engaging, while still being relatively simple, such that its difficulty level can be manipulated via adjusting one variable (Keller & Bless, 2008).

In line with previous studies (e.g., Keller & Bless, 2008; Tozman et al., 2015), flow was induced via manipulating challenge optimality. The current study started with an initial session (session 0), during which participants were instructed to familiarise themselves with the game. In session 0, difficulty variation was set at normal mode regardless of conditions. Session 0 served to gauge each participant’s skill levels: the highest difficulty level each participant attained during this session was taken as a proxy of their skill levels. Starting from the second session, the game randomly entered one of the 3 distinct playing modes, depending on the experimental condition: In the boredom condition, the level was fixed at level 1 or the proxy skill level minus 3, whichever was higher; in the overload condition, the level was set at the proxy skill level plus 5, and could potentially increase (but never decrease) if the participant managed to clear rows, with a maximum value of 10; in the optimal condition, the level was set at the participants’ proxy skill level and continued to self-adjust to fit the participant’s skill level—If the player successfully clears 5 lines or more, the difficulty level increases by 1 stage. If the player accomplished 3 lines or less, the difficulty level decreases by 1 stage. Thus, the boredom condition consistently requires less swift responses to succeed (i.e., requiring less mental effort), while the optimal condition consistently requires more of such responses, and the overload condition requires the largest number of swift responses. Manipulation checks were conducted.

Measurements

Overall Flow. At the end of the experiment, the participants were asked to complete the flow state scale (FSS; Jackson & Eklund, 2002). The FSS is a widely used and validated 36-item questionnaire, rated on a 5-point Likert scale, asking respondents whether their experience during a specified activity (in our case, the experimental task) has the flow characteristics described. It consists of 9 subscales, 1 for each of the components of flow. An overall flow score for each participant is computed by obtaining the average score of the 36 items.

Positive and Negative Affect Schedule. The Positive and Negative Affect Schedule (the PANAS) is a 20-item scale developed by Watson et al., (1988). It uses 10 items to measure state positive affect and 10 items to measure state negative affect, with the respondents being asked to rate the degree to which they felt a specified emotion on a 5-point scale (5 being very much and 1 being very slightly or not at all). The PANAS has been widely used in emotion research. The 10 items for PA were used as a measure for PA in the current study.

Procedure

The study utilised a 3 x 4 design, consisting of 3 experimental groups—the boredom group, the overload group, and the optimal group, with the focal variables (PA and flow) measured at each of the four timepoints, i.e., the end of each session, t1, t2, t3, and t4.

Participants were randomly assigned to groups and did not know which group they were in. The monitor was used to display the Tetris game, which was written in MATLAB. As the participants entered the laboratory, they were briefed and instructed that this is an experiment about emotional and cognitive processes involved in video game playing. The concept of flow was not mentioned. After that, they were seated in front of their computers, via which the questionnaires and the Tetris task were delivered. After that, the experiment began. Session 0 lasted 8 minutes. After the play session, the participants responded to a short flow scale (a 9-item version of FSS) and the PANAS. They were then given a 2-minute break during which they are free to choose between taking a break or practicing the Tetris game on their own.

After session 0, the three experimental groups started to diverge in terms of their experience of difficulty. The Tetris game they played from that point on was (unknown to them) of the difficulty that corresponded to their assigned group. This process of “8 minutes on the game and then 2-minute break” was repeated 4 times. At the end of the final session, the participants responded to the FSS asking about their overall experience. After that, the experimenter thanked the participants for their contributions and debriefed them. The experimental procedure was visually presented in Figure 2.

Figure 2. The Flow Chart of Study 1, With Time Points at Which Measurements Were Taken Specified.

Note. The PANAS and short flow scale were administered at the end of each gameplay session but before the corresponding break. The FSS-2 measuring overall flow was administered after the end of the last session’s break.

Results

Descriptive statistics and alphas for the focal variables are shown in Table 1.

Table 1. Study 1 Descriptive Statistics.

Hypotheses Testing

Complete results are in the Appendix. The path model is presented in Figure 5. This model was analysed using AMOS SPSS 26 and showed desirable model fits. It had χ² (df = 33) = 34.4, RMSEA = .017, GFI = .946, CFI = .998. All of these indices were considered well within the acceptable range. Thus, we concluded that our model provided a good fit for the data.

H1 stated that challenge optimality causes greater PA. An one-way ANOVA was conducted to compare overall PA. The result was significant, F(2, 144) = 29.33, p < .001, η² = .294 (Figure 3). Post hoc tests with Bonferroni correction showed that the optimal group (M = 2.34) scored higher than the boredom group (M = 1.37), Cohen’s d = 1.568, p < .001, and the overload group (M = 1.91), Cohen’s d = 0.624, p < .001, whilst the boredom group scored lower than the overload group, Cohen’s d = 0.968, p < .001.

We also measured PA during session 0 (during which all participants experienced the difficulty setting). A two-way repeated measure ANOVA showed that there was an interaction between group and time point, with PA being the DV, F(2, 144) = 26.79, p < .001, partial η² = .275 (Figure 4). Post-hoc test with Bonferroni correction showed that the optimal group differs from the boredom group, mean difference = .434, p = .001, and also from the overload group, mean difference = .359, p = .008, but the boredom group and the overload group did not differ from each other, mean difference = .075, p = 1.000. Further investigation using one-way ANOVA revealed that participant PA in session 0 did not differ across the three groups, F(2, 144) = .56, p = .571, η² = .008, but did at the final session, F(2, 144) = 26.57, p < .001, η² = .274. As (1) we have manipulated the cause variable (difficulty optimality) and (2) we have shown that the effect variable (PA) differs after but not before the onset of the manipulation, we concluded that the relationship between challenge optimality and PA satisfied both criteria for causality in psychology (Kazdin, 2007). H1 is supported. The results suggested that DDA-elicited optimal challenge causes increased positive emotional experience.

Figure 3. ANOVA Comparing the Overall PA of the Three Groups.

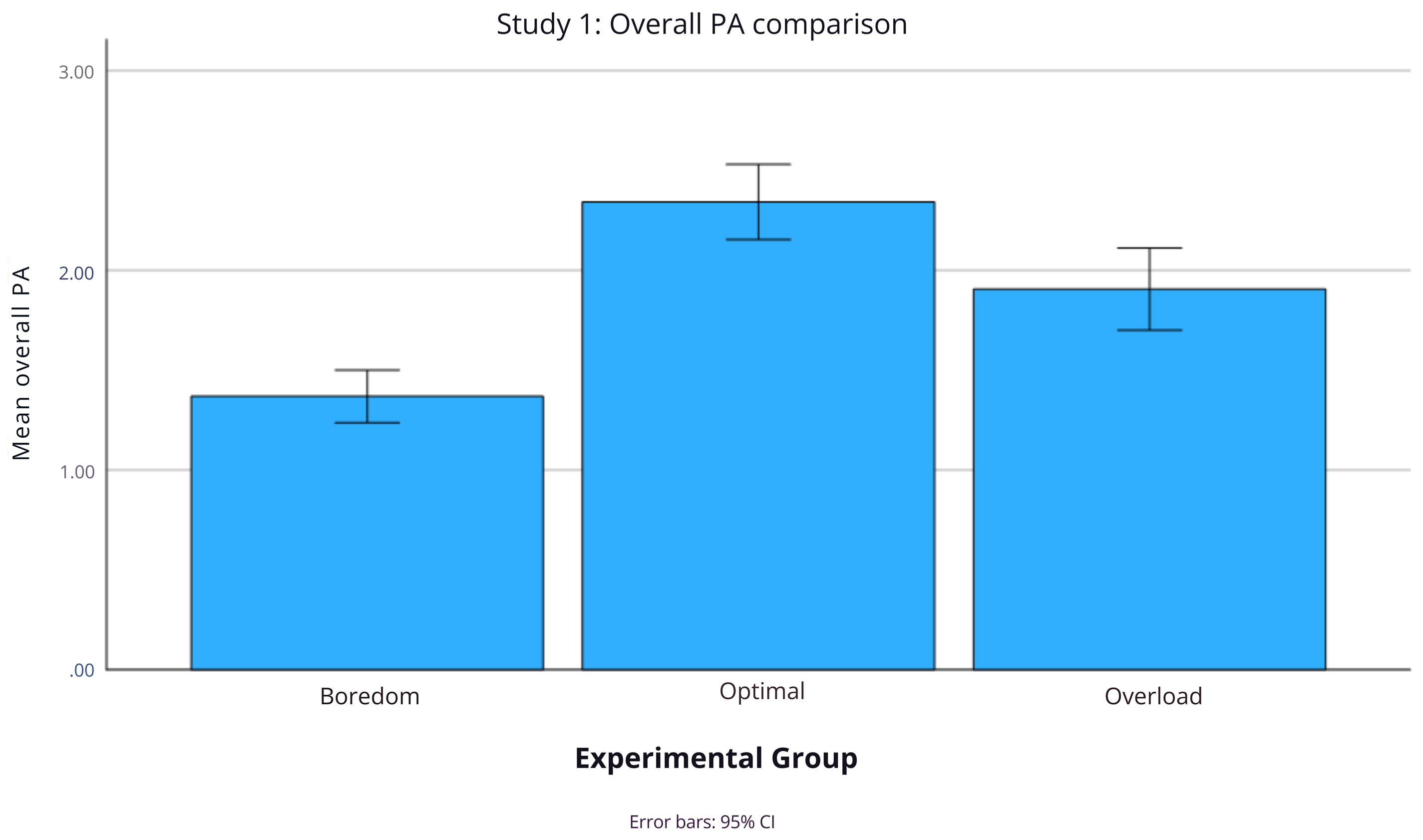
Figure 4. Two-Way Repeated Measure ANOVA, Showing How PA Changes Before and After the 4 Sessions.

H2 stated that PA is positively associated with concurrent flow (flow at the same time point as the PA in question). H2 was mostly supported: most of the paths between PA and concurrent flow were significant and positive. The sole exceptions were PA at t2 -> flow at t2 for non-optimal groups, PA at t3 -> flow at t3 for overload group, and PA at t4 -> flow at t4 for boredom group, which were non-significant. H2 is supported. The results suggested that current positive emotional experience is positively associated with concurrent flow.

H3 stated that current PA is positively associated with future PA. H3 was supported: When PA was used to predict PA at the time point that immediately followed, e.g., PA at t1 -> PA at t2, PA at t2 -> PA at t3, the effect was significant and positive regardless of groups. However, when PA at a time point was used to predict PA further in the future, e.g., PA at t1 -> PA at t3, only 2 out of the 9 paths were significant, i.e., PA at t1 -> PA at t3 for the optimal group and PA at t2 -> PA at t4 for the overload group. H3 is supported. The results suggested that current positive emotional experience is positively associated with future positive emotional experience.

Figure 5. Path Analysis Results.

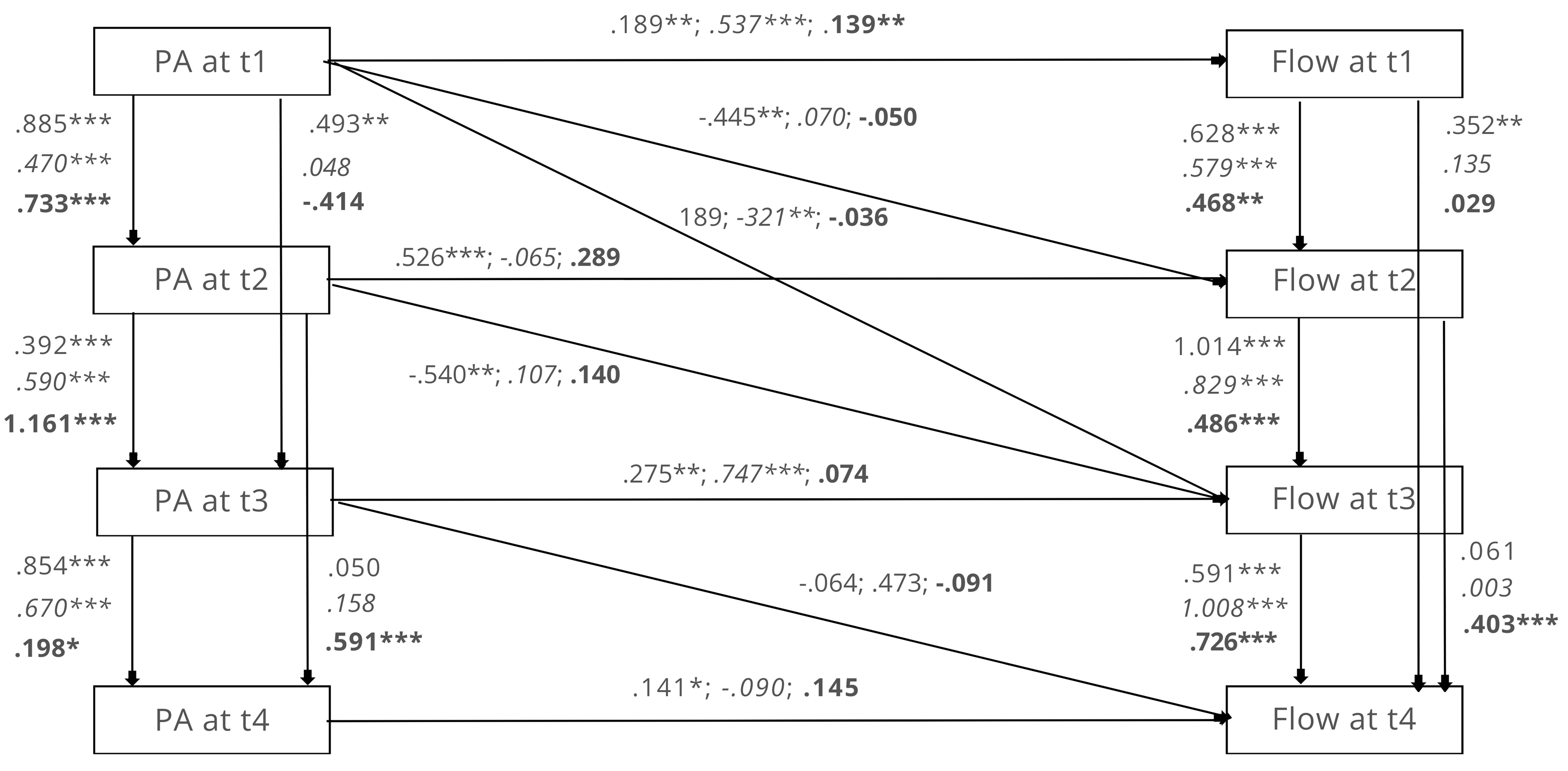
Note. *p < .05, **p < .01, ***p < .001. Each path has three numbers, representing its coefficients across the three groups. Normal font = optimal group, italic = boredom group, bold = overload. Model Fit: RMSEA = .017; GFI = .946, CFI =.998; CMIN = 34.372, p > .05, df = 33; Using PA at time 1 to predict flow at time 4 has been attempted, but the path failed to reach significance in any group. Thus, we removed it from the final model for a better degree of freedom value.

Multigroup Path Analysis

Our model contains PA and flow at different time points which are all at the same level. For this reason, we chose to perform a multigroup analysis which provides the capacity to assess each of the paths within the different levels of difficulty. The model was not multi-level and featured no covariates.

H4a and H4b suggested that the effect current PA has on future flow is moderated by challenge optimality. We used the method of equality constraint to test for moderation effects. First, the overall chi-square value (χ² = 34.37, df = 33) was obtained for the model. Next, we constrained the paths from each of the PA variables to flow at timepoints later than that PA variable to be equal across groups. Then the new chi-square value (χ² = 58.60, df = 39) was obtained. A chi-square comparison of the two models revealed that the difference was significant, p < .001. Thus, constraining the paths to be different across groups resulted in a worsened model fit, confirming our hypotheses that at least some of the paths between PA variables and subsequent flow differ between the three groups.

Further investigation also generally confirmed the hypotheses: H4a and H4b stated that the paths (PA predicting future flow) would be more negative if a person currently experiences optimal challenge compared to a person who currently experiences overload or boredom. These two hypotheses were mostly supported: There were six paths from PA to future flow in the model, PA at t1 -> flow at t2, PA at t1 -> flow at t3, PA at t1 -> flow at t4, PA at t2 -> flow at t3, PA at t2 -> flow at t4, PA at t3 -> flow at t4. For the optimal groups, all but one (namely PA at t3 -> flow at t4) of the paths where PA is used to predict flow at the next time point, i.e., PA at t1 -> flow at t2 and PA at t2 -> flow at t3, were significant and negative, as expected. The same paths for neither overload nor boredom groups were significant. It was noted that PA at t1 -> flow at t3 for boredom group was the only path where PA significantly predicts flow at a time point further than the next one. We conclude that the current study provides overall support for H4a and H4b. Positive emotional experience is negatively associated with future flow, unless the person is experiencing overly high difficulty.

We also conducted a nested model analysis. Some might argue that a simpler model might account for the observed data just as well as the more complex one. Thus, we ran a nested model that is identical to the one in Figure 5, except all paths from past PA to future flow were removed. The resultant model had worse model fit indices, χ² (df = 42) = 68.10, RMSEA = .066, GFI = .904, CFI = .968.

Multicollinearity

Linear regressions were conducted to check for multicollinearity issues. For each flow variable, a linear regression was conducted using predictor variables in the path model as independent variables. None of the VIF statistics was greater than 10 (Alin, 2010). To be more specific, the VIF statistics were summarised in Table 2. Thus, we conclude that there is no multicollinearity issue.

Table 2. Study 1 Multicollinearity Tests.

Study 2

Study 2 was conducted to clarify the nature of the link between past PA and current flow. There are at least two explanations for why past PA predicts current flow: (1) participants could be basing their perception of current difficulty by (explicitly or implicitly) using past PA as an indicator of past difficulty, or (2) participants were not remembering past difficulty and the influence was largely emotional—previous PA resulted in physiological changes that reduced current flow. In Study 2, we manipulate the variable of ‘previous difficulty’ by varying difficulty levels at the within-person level as opposed to Study 1, in which difficulty remains constant for each individual participant. If players base their perception of current difficulty by explicitly considering information on past difficulty, then we should expect actual past difficulty levels to influence flow. Thus, two groups that experience identical current difficulty levels, but different past difficulty levels, should have different perceived levels of current difficulty and thus experience different levels of current flow.

In Study 2, participants were divided into four groups: (1) optimal-optimal group, who experienced optimal challenge throughout the experiment, (2) overload-overload group, who experienced overload throughout the experiment, (3) optimal-overload group, who experienced optimal challenge in the first half of the experiment and overload in the second half, and (4) overload-optimal group, who experienced overload in the first half and optimal challenge in the second half.

In Study 2, aside from trying to replicate the previous findings, we also seek to test the following hypotheses:

H5: Previous experience with optimal challenge would improve flow, as compared to previous experience of overly high difficulty.

Methods

Participants

A total of 338 (approximately 44% male; 56% female) participants were recruited over the course of two semesters in the second half of 2019 and early 2020. All of them were students at the University of New South Wales, Australia. Most (242) of them were rewarded with $20 AUD upon completion of the study, while the others were recruited via advertising to the cohort of undergraduate students who attended an entry-level management course. Participants recruited via the latter channel were rewarded with credits for their course. The experimental procedure is visually presented in Figure 6.

Figure 6. The Flow Chart of Study 2.

Procedure

The experimental task, procedures, and measurements are identical to those in Study 1, except Study 2 uses a 4 x 4 design, with the four experimental groups being the optimal-optimal group (participants who experienced optimal challenge throughout), optimal-overload group (optimal challenge in the first half and overload in the second half), overload-optimal group (overload in the first half and optimal challenge in the second half), overload-overload (overload throughout). There are four time points of measurement.

Results

Manipulation Check

An independent sample t-test was conducted to compare the groups which experienced optimal challenge in block 1, i.e., optimal-overload and optimal-optimal, against the groups which experienced overly difficult challenge in block 1, i.e., overload-overload and overload-optimal, on the level of flow. The result was significant, t = 9.48, p < .001, with the optimal group scoring higher on flow (M = 3.18) than the overload group (M = 2.57). Thus, we conclude that the manipulation was effective in inducing heightened levels of flow for participants who experienced optimal levels of challenge in the first half of the experiment.

Another independent sample t-test was conducted to compare the two groups on PA. The result was significant. For block 1, t = 4.90, p < .001, with the optimal group scoring higher on PA at the first session (M = 2.76) than the overload group (M = 2.31). For block 2, t = 6.09, p < .001, with the optimal group scoring higher on PA at the second session (M = 2.64) than the overload group (M = 2.06). Moreover, there was no difference between the two groups on flow before the difference in difficulty setting set in (i.e., during session 0), t = −1.00, p = .32.

Table 3. Descriptive Statistics.

Hypotheses Testing

Complete results are in the Appendix. T-tests showed that participants who experienced optimal challenge in the first half scored higher on PA, at both block 1 and block 2, compared to those who experienced overload in the first half, and skill-challenge optimality was experimentally manipulated in our study. In contrast, an one-way ANOVA showed that none of the 4 groups differed from the others significantly in terms of PA immediately after the test session, F(3, 338) = 1.48, p = .219, η² = .013. In this model, we combined the PA scores at time 1 and time 2, forming “PA at the first half of the experiment”. Then we similarly combined the flow scores at time 1 and time 2, combined the PA scores at time 3 and time 4, and combined the flow scores at time 3 and time 4. This enabled us to test the model without it being overwhelmed with excessive numbers of paths. H1 is once again supported. Also, regardless of group, PA could positively predict concurrent flow (H2) and PA could positively predict future PA (H3).

To further investigate, a two-way 4x2 repeated measure ANOVA was conducted to compare the four groups on PA during the second half (4 groups, 2 time points, only time 3 and time 4), with PA having two levels (PA at time 3 and PA at time 4). The between-subject effect of group was significant, F(3, 338) = 11.892, p < .001, partial η² = .097. For the within-subject contrast, there was a main effect of time, F(334, 338) = 25.726, p < .001, partial η² = .072, but there was no time x group interaction, F(3, 338) = .208, p = .891, partial η² = .002. Post Hoc tests with Bonferroni correction showed that, optimal-optimal group and overload-optimal group did not differ on PA, Cohen’s d = 0.268, p = .410. Optimal-overload group and overload-overload group did not differ on PA, Cohen’s d = 0.009, p = 1.000. Overload-optimal group and overload-overload group do differ on PA (averaged across time 3 and time 4), Cohen’s d = 0.795, p = .005. Optimal-optimal group and optimal-overload group also differ on PA (also averaged across time 3 and time 4), Cohen’s d = 0.488, p < .001. Thus, it seems that PA depends largely on current challenge optimality, and past challenge optimality has minimal effect on PA.

To investigate whether past objective difficulty could impact current perception of difficulty, we evaluate flow in block 2. We conduct another two-way 4x2 repeated measure ANOVA. There was no significant main effect by time, F = 2.566, df = 1, p = .110. There was a highly significant between-subject effect from group, F = 38.954, df = 1, p < .001, but no within-subject effect. We then conducted post hoc tests with Bonferroni correction. The results generally suggest that past objective difficulty does not influence current flow (Figure 8): The comparison between optimal-optimal group and overload-optimal group showed no significant differences, mean difference = .186, p = .441. The comparison between optimal-overload group and overload-overload group showed that the two groups did not differ on flow at all, mean difference = .107, p = 1.000. H5a and H5b are hence not supported. This result suggests that participants’ perceived difficulty (which determines the level of flow) does not seem to be influenced by past objective difficulty. Therefore, it is not very likely that PA’s effect on future flow is due to participants using PA as a source of information to perceive the game’s difficulty. Instead, the effect is likely due to primarily affective processes, e.g., PA predisposes participants to perceive difficulty in a certain way, thus influencing future flow.

Figure 7. Path Analysis Results.

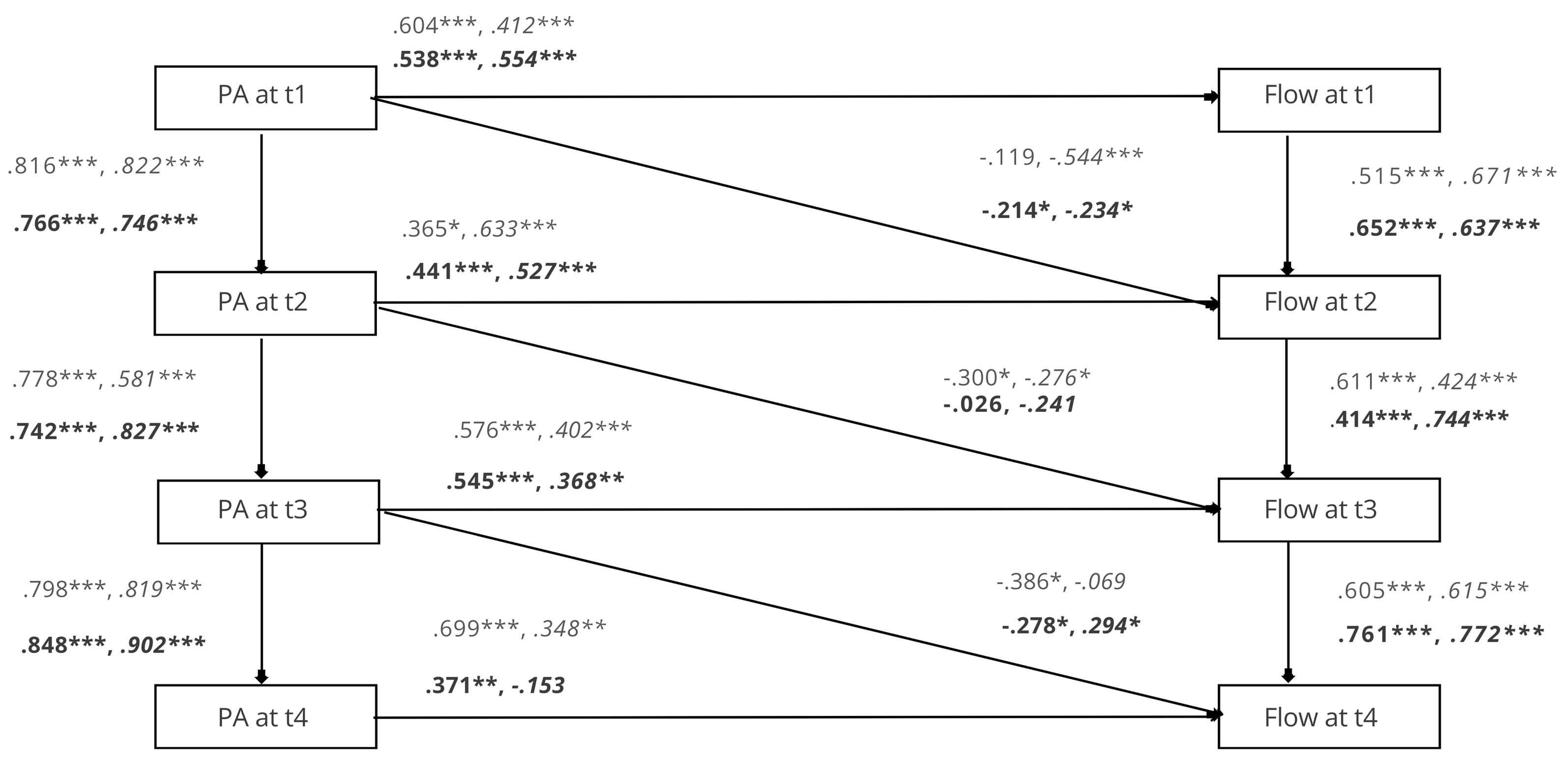
Note. *p < .05, **p < .01, ***p < .001. Each path has four numbers, representing its coefficients across the four groups. Normal font = optimal-optimal group, italic = optimal-overload group, bold = overload-overload group, bold and italic = overload-optimal group. Model Fit: RMSEA = .061; CFI = .964; CMIN = 135.705, df = 60.

Figure 8. The t-test Comparing Groups on Flow in the Second Half.

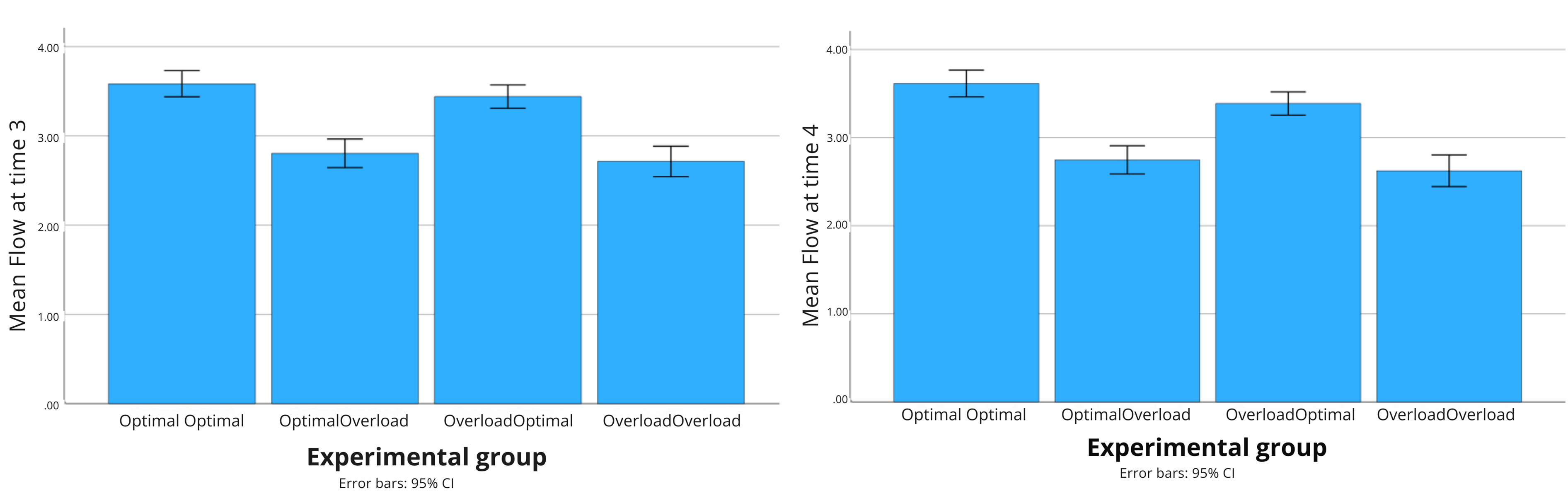
                                                     Note. Labelling: OptimalOptimal = the optimal-optimal group; OptimalOverload = the optimal-overload group;
                                                             OverloadOptimal = the overload-optimal group; OverloadOverload = the overload-overload group.

We then conducted multi-group path analysis, using the model depicted in Figure 7 and the four experimental groups as grouping variables. We noticed that the path from past PA to current flow differs across the experimental groups in standardised betas. We conducted equality constraint analysis to investigate this. First, the overall chi-square value (χ² = 135.705, df = 60) was obtained for the model. Next, we examined the path PA at time 1 -> flow in time 2 and the path PA at time 3 -> flow in time 4. We chose not to make any hypothesis about the path PA at time 2 -> flow in time 3, because change in difficulty setting was involved. We then attempted equality constraint. Constraining the path PA at time 1 -> flow in time 2 resulted in a slightly worse chi-square value (χ² = 141.008, df = 63), which was not significant. Constraining the path PA at time 3 -> flow in time 4 also resulted in a slightly worse chi-square value (χ² = 149.924, df = 63), with the difference being significant at p < .05. This suggests that the PA at time 3 -> flow in time 4 path differs between groups.

Next, we examined the path. The path from PA at time 1 -> flow in time 2 was highly significant and negative across groups, except for the optimal-optimal group, where it was negative albeit non-significant. The path PA at time 3
-> flow in time 4 was highly significant in optimal-optimal group and overload-optimal group, while being non-significant in optimal-overload and positive in the overload-overload. Overall, this seems to be in line with our hypothesis that the link between past PA and future flow tend to be more negative when the difficulty level is optimal, compared to when the difficulty is overload. H4a and H4b received support.

Multicollinearity

Linear regressions were conducted to check for multicollinearity issues. For each flow variable, a linear regression was done using predictor variables in the path model as independent variables. None of the VIF statistics was greater than 10. Thus, we conclude that there is no multicollinearity issue.

Table 4. Multicollinearity Tests.

Alternate Models

We also considered alternate models for our data. It has often been suggested that flow-inducing activities are often regarded as highly satisfying (Engeser & Baumann, 2016). Thus, these activities could, at least in theory, elicit PA. This means current flow might predict future PA. To test this possibility, we tested two alternate models: (1) a cross-lagged model where current PA and current flow have paths towards each other and each has paths towards future PA and future flow; and (2) a reverse model where current flow has paths towards current PA and future flow, but current PA does not have path towards future flow. Using Study 1’s data, the results showed that the two alternate models have worse fit indices than the model we used. The cross-lagged model has RMSEA of .261 while the reverse model has RMSEA of .062. The latter value, while acceptable, was worse than our proposed model’s (RMSEA = .017). Using Study 2’s data, we found a similar pattern, with the reverse model having a somewhat acceptable but worse fit (RMSEA = .075), while the cross-lagged model has unacceptable fits (RMSEA = .131), compared to the proposed model’s RMSEA of .061. Due to these fit indices, we decided to focus on the models based on our hypotheses, where current PA predicts future flow but current flow does not predict future PA.

Discussion

Based on our findings, we organise our discussion into three sections: summary of the key findings and discussion of their relations to the literature, suggestions for game design, and limitations.

Findings With Regard to the H4s

H4a and H4b are our most novel hypotheses. We argued that current PA could predict future flow and this link is moderated by challenge optimality. Namely, this link would be particularly negative in the boredom and optimal groups, as compared to the overload group. H4a and H4b were mostly supported.

One possible explanation for this relationship is stress. Some recent studies (Peifer et al., 2011, 2014) have attempted to investigate the role of stress in flow experience. Their general finding was that flow seemed to be associated with moderate levels of stress—if the game is too easy, the stress level is low, so is the level of flow. If the game is too difficult, the stress level is high, and the level of flow is low. The highest levels of flow occurred at medium levels of stress, i.e., an inverted U-shape (Peifer et al., 2011, 2014). This is in accordance with the idea that flow requires (or at least is facilitated by) difficulty. Many studies in the B&B literature demonstrated that positive emotional experience could reduce stress. Such studies have attempted to experimentally induce stress in participants. After the stress inducer, some participants were given manipulations that induced PA, while the others received manipulations that induced neutral or negative emotions. Their results were that participants with induced PA underwent faster cardiovascular recovery from stress. B&B researchers termed this “the undoing effect of positive emotions on stress“ (Fredrickson & Levenson, 1998; Fredrickson et al., 2000). Given that the flow state is more compatible with moderate levels of stress, it is plausible that for participants in non-overload conditions, the stress reduction effects of PA reduce subsequent flow. We cannot test this hypothesis, as we did not measure stress. However, we strongly recommend future studies to evaluate this possibility. If confirmed, this will be a valuable addition to the dynamic model of flow (Kotler et al., 2022).

The hypothesis that PA reduces subsequent flow via reducing stress suggests that PA and flow form a negative feedback loop: imagine a player is playing a game that offers optimal challenge, resulting in a high level of flow. PA, being an effect of optimal challenge and a correlate of flow, also rises. PA then exerts influence on stress, reducing the likelihood of subsequent flow. This resulted in a feedback loop in which the gaming session lasts a finite amount of time—PA reducing stress means that flow eventually diminished and given that flow is positively associated with the motivation to play, the player eventually put down the controller. This might have implications for video game addiction research: Many video game addiction studies suggested that addicts frequently reported using games to escape negative emotions (e.g., Weinstein, 2010). These individuals might experience high negative emotions and thus have difficulty experiencing PA during their gameplay. This in turn disrupts the loop that causes players to spontaneously stop playing.

Minor Findings

Challenge optimality could cause changes in PA (H1). Past studies have already established the positive associations between flow and PA (Chiang et al., 2008, 2011; Schüler, 2007). These studies were typically correlational and thus could not establish causal relations (e.g., Hatfield et al., 2006). Some recent studies have attempted to use experimental manipulation to establish causal relations (Huskey et al., 2018). Our study has used experimental manipulation and provided support for a causal relationship between optimal challenge and PA, corroborating works such as Huskey et al. (2018).

Regarding H2, we found that PA is positively associated with concurrent flow, regardless of challenge optimality in line with previous studies (Chiang et al., 2008, 2011; Konradt et al., 2003; Rogatko, 2009). Our study, however, took one small step further—these past studies generally did not use experimental study designs with multiple groups. By conducting an experiment, we have helped establish that not only could PA predict flow, but also that PA could do so regardless of difficulty setting.

Current PA could positively predict future PA (H3). This was in line with the idea of the “upward spiral of positive affect” (Burns et al., 2008; Ramsey & Gentzler, 2015). Our finding is once again an expansion upon extant ideas—our study shows that, at least in the context of video gaming, the ability for PA to predict future PA does not seem to last for more than 10 minutes (the duration of one session), since for the most part, current PA could only predict PA in the session that immediately followed.

Also, we noted that across both studies, there seems to be a tendency for PA and flow to decrease over time (as shown in the descriptive statistics in Table 1 and Table 3). This might indicate that participants, regardless of group, felt slightly more bored of the game over the course of an hour. We did not directly measure boredom. Nonetheless, researchers might want to investigate this in future studies.

Suggestions for Game Design and Research

At the most basic level, this study has implications for predicting player experience. There is a rich literature on predicting “fun” (which typically at least includes flow as a key component; Beume et al., 2008) based on game characteristics. Our study showed that PA at previous time points is a key predictor of flow. Researchers interested in player experience prediction likely need to take this into account. For example, attempts to predict player flow using neural networks (e.g., Maier et al., 2019) might need to include “previous PA” as a predictor variable.

Salient affective stimuli are ubiquitous in digital games, such as in-game characters expressing emotions (e.g., for a review, see De Byl, 2015). Our study’s core message is that game designers should be cautious about using salient affective stimuli in conjunction with difficulty manipulations. Namely, the current results suggest that stimuli that elicit PA will reduce subsequent player flow under conditions of low or optimal difficulty. Moreover, it seems that PA is unlikely to reduce subsequent flow under conditions of high difficulty. Future studies should likely further develop the concept of PA forming a negative feedback loop with flow and how to optimise the amount of time players spend on gaming, i.e., the amount of time should ideally be high enough for a game to be profitable, but also not so high as to result in addictive behaviour.

Limitations

While this study has produced some interesting findings, it does have its limitations. Firstly, in both Study 1 and 2, the entire experiment occurred over the course of an hour. Thus, while it has given information on the interplay between PA and flow within such a timeframe, it could not give information about such interplay over the courses of days or weeks—when gaming is typically driven by recurrently playing a game each day (or every few days) over the courses of weeks and months (Sherry et al., 2006). Indeed, we noted that our results seemed to contradict those obtained by some other flow researchers. R. Wu et al. (2021) also attempted to investigate how current PA predicts future flow. In contrast to our studies, however, they reported that a cross-lagged model fit their data and that in their studies, current PA positively predicts future flow. One potential explanation could be that Wu et al.’s study spanned a much longer timeframe, i.e., 2 years, while our studies were completed in about an hour. Our findings seem to suggest that the negative effect PA has on future flow might be short-term, lasting no more than 15 to 20 minutes. This is in accordance with the idea of PA reducing subsequent flow via reducing stress, as the “undoing effect of PA on stress” is also known to occur via relatively short time frames, spanning minutes, or hours at most. Thus, if two time points were as far away as several months, it is unlikely for that effect to be significant. We also note that Wu et al.’s study was conducted in an education context instead of a gaming one. Future studies might want to explore the PA-flow interplay in multiple sections over the course of days and weeks.

Some variables were not measured and might have exerted confounding effects, such as the participants’ prior exposure to Tetris and how participants’ skill levels might have changed during the course of the experiment (especially since they were allowed to play and thus practice during the breaks). Moreover, some participants in Study 2 received monetary incentives instead of course credits. Future studies likely should measure these variables and consider them as control variables in their models.

Potential issues with multicollinearity might also be of concern. While none of our VIF statistics were outside the acceptable limit, a few were quite close to being greater than 6.0 (a stricter VIF requirement used by many; Clark Jr, 2013), being in the 4.0 to 5.0 range. This might cause issues with estimating the effects of each independent variable.

Lastly, there is doubt with regards to whether our findings could be generalised to certain video game genres. Horror games, for instance, are quite unusual in that they are designed with the explicit goal of inducing negative emotions (most prominently fear; Habel & Kooyman, 2014). Given that (1) fear has been highlighted as the key source of enjoyment in such games, and that (2) PA is negatively associated with negative emotional experiences, it is likely that flow (or other enjoyment indicators) in horror games might be linked to PA in a different way.

Concluding Remarks

Our results suggest that manipulation of challenge optimality causes changes in the level of PA. PA can not only predict concurrent flow, but also predict future flow. However, the direction of this effect is dependent on whether the skill-challenge compatibility is optimal. Our data suggest that PA’s effect is particularly negative on future flow when skill-challenge compatibility is optimal, a novel finding that is also somewhat counterintuitive. This resulted in the concept of flow and PA forming a negative feedback loop with each other. Our results will likely have important implications for the design of affective experience in digital games.

Conflict of Interest

The authors have no conflicts of interest to declare.

Authors’ Contribution

Man-Chung Fung: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, software, validation, visualization, writing—original draft, writing—review & editing. Christopher Jackson: conceptualization, formal analysis, funding acquisition, methodology, resources, supervision, writing—review & editing.

Acknowledgement

This project was partly funded by the Small Project Grant provided by the University of New South Wales Business School.

Appendix

Table A1. Study 1: Boredom.

Table A2. Study 1: Optimal.

 Table A3. Study 1: Overload.

Table A4. Study 2: Optimal Optimal.

Table A5. Study 2: Optimal Overload.

Table A6. Study 2: Overload Optimal.

Table A7. Study 2: Overload Overload.